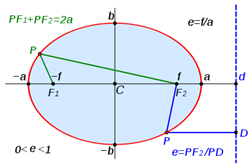
Perbedaan antara hiperbola dan elips
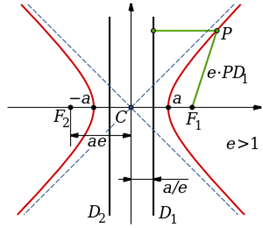
Hiperbola vs elips
Ketika kerucut dipotong pada sudut yang berbeda, kurva yang berbeda ditandai oleh tepi kerucut. Kurva ini sering disebut bagian kerucut. Lebih tepatnya, bagian kerucut adalah kurva yang diperoleh dengan memotong permukaan kerucut melingkar kanan dengan permukaan bidang. Pada sudut persimpangan yang berbeda, bagian kerucut yang berbeda diberikan.
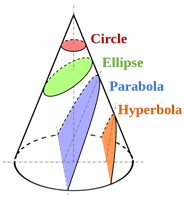
Baik hiperbola dan elips adalah bagian kerucut, dan perbedaannya mudah dibandingkan dalam konteks ini.
Lebih lanjut tentang elips
Saat persimpangan permukaan kerucut dan permukaan bidang menghasilkan kurva tertutup, ia dikenal sebagai elips. Ini memiliki eksentrisitas antara nol dan satu (0 Segmen garis yang melewati fokus dikenal sebagai sumbu utama, dan sumbu tegak lurus terhadap sumbu utama dan melewati pusat elips dikenal sebagai sumbu minor. Diameter sepanjang setiap sumbu dikenal sebagai diameter melintang dan diameter konjugat masing -masing. Setengah dari sumbu utama dikenal sebagai sumbu semi-mayor, dan setengah dari sumbu minor dikenal sebagai sumbu semi-minor. Setiap titik f1 dan f2 dikenal sebagai fokus elips dan panjangnya F1 + PF2 = 2a , Di mana P adalah titik sewenang -wenang pada elips. Keanehan e didefinisikan sebagai rasio antara jarak dari fokus ke titik sewenang -wenang ( PF2 ) dan jarak tegak lurus ke titik sewenang -wenang dari Directrix (PD). Ini juga sama dengan jarak antara dua fokus dan sumbu semi-mayor: e = PF/PD = f/a Persamaan umum elips, ketika sumbu semi-mayor dan sumbu semi-minor bertepatan dengan sumbu kartesius, diberikan sebagai berikut. X2/A2 + y2/B2 = 1 Geometri elips memiliki banyak aplikasi, terutama dalam fisika. Orbit planet di tata surya adalah elips dengan matahari sebagai satu fokus. Reflektor untuk antena dan perangkat akustik dibuat dalam bentuk elips untuk memanfaatkan fakta bahwa emisi apa pun yang membentuk fokus akan menyatu pada fokus lainnya. Lebih lanjut tentang hiperbola Hiperbola juga merupakan bagian kerucut, tetapi terbuka. Istilah hiperbola dirujuk ke dua kurva terputus yang ditunjukkan pada gambar. Daripada menutup seperti elips lengan atau cabang hiperbola berlanjut hingga tak terbatas. Titik -titik di mana kedua cabang memiliki jarak terpendek di antara mereka dikenal sebagai simpul. Garis yang melewati simpul dianggap sebagai sumbu utama atau sumbu transversal, dan itu adalah salah satu sumbu utama hiperbola. Dua fokus parabola juga terletak pada sumbu utama. Titik tengah garis antara dua simpul adalah pusat, dan panjang segmen garis adalah sumbu semi-mayor. Pembagi tegak lurus dari sumbu semi-mayor adalah sumbu utama lainnya, dan dua kurva hiperbola simetris di sekitar sumbu ini. Eksentrisitas parabola lebih besar dari satu; e> 1. Jika sumbu utama bertepatan dengan sumbu Cartesian, persamaan umum hiperbola adalah dari bentuk: X2/A2 - y2/B2 = 1, Di mana A adalah sumbu semi-mayor dan B adalah jarak dari pusat ke salah satu fokus. Hiperbola dengan ujung terbuka menghadap sumbu x dikenal sebagai hiperbolas timur-barat. Hiperbola serupa juga dapat diperoleh pada sumbu y. Ini dikenal sebagai hiperbola sumbu y. Persamaan untuk hiperbolas seperti itu mengambil formulir y2/A2 - X2/B2 = 1 Apa perbedaan antara hiperbola dan elips? • Kedua elips dan hiperbola adalah bagian kerucut, tetapi elips adalah kurva tertutup sedangkan hiperbola terdiri dari dua kurva terbuka. • Oleh karena itu, elips memiliki perimeter terbatas, tetapi hiperbola memiliki panjang yang tak terbatas. • Keduanya simetris di sekitar sumbu utama dan minor mereka, tetapi posisi Directrix berbeda dalam setiap kasus. Di elips, ia tergeletak di luar poros semi-mayor sementara, pada hiperbola, terletak di poros semi-mayor. • Eksentrisitas dua bagian kerucut berbeda. 0 eHiperbola > 0 • Persamaan umum dari kedua kurva terlihat sama, tetapi mereka berbeda. • Para bisektor tegak lurus dari sumbu utama memotong kurva dalam elips, tetapi tidak pada hiperbola. (Sumber Gambar: Wikipedia)