Perbedaan antara Laplace dan Fourier Transforms

Laplace vs Fourier Transforms
 

Transformasi Laplace dan transformasi Fourier adalah transformasi integral, yang paling sering digunakan sebagai metode matematika untuk menyelesaikan sistem fisik yang dimodelkan secara matematis. Prosesnya sederhana. Model matematika yang kompleks dikonversi menjadi model yang lebih sederhana dan dapat dipecahkan menggunakan transformasi integral. Setelah model yang lebih sederhana dipecahkan, transformasi integral terbalik diterapkan, yang akan memberikan solusi untuk model asli.

Misalnya, karena sebagian besar sistem fisik menghasilkan persamaan diferensial, mereka dapat dikonversi menjadi persamaan aljabar atau ke tingkat yang lebih rendah dengan mudah diselesaikan persamaan diferensial menggunakan transformasi integral. Maka menyelesaikan masalah akan menjadi lebih mudah.

Apa Transformasi Laplace?

Diberi fungsi F (T) dari variabel nyata T, Transformasi Laplace-nya didefinisikan oleh integral [latex] f (s) = \\ int_ 0^\\ infty e^-st f (t) dt [/lateks] (kapan pun ada), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang), yang ada), yang ada), yang ada), yang ada), yang ada), adalah fungsi dari variabel yang kompleks S. Biasanya dilambangkan dengan l F (T). Transformasi Laplace terbalik dari suatu fungsi F(S) dianggap sebagai fungsinya F (T) sedemikian rupa sehingga l F (T) = F(S), dan dalam notasi matematika biasa kita tulis, l ^-1F(S) = F (T).Transformasi terbalik dapat dibuat unik jika fungsi nol tidak diperbolehkan. Seseorang dapat mengidentifikasi keduanya sebagai operator linier yang didefinisikan dalam ruang fungsi, dan juga mudah untuk melihat itu, l ^-1L F (T) = F (T), jika fungsi nol tidak diperbolehkan.

Tabel berikut mencantumkan transformasi Laplace dari beberapa fungsi yang paling umum.

Apa Transformasi Fourier?

Diberi fungsi F (T) dari variabel nyata T, Transformasi Laplace-nya didefinisikan oleh integral [latex] f (\\ alpha) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ infty^\\ infty e^i \\ alpha t f (t) dt [/latex] (kapan pun ada), dan biasanya dilambangkan dengan f F (T). Transformasi terbalik f ^-1F(α) diberikan oleh integral [latex] f (t) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ infty^\\ infty e^ -i \\ alpha t f (\\ alpha) d \\ alpha [/latex]. Transformasi Fourier juga linier, dan dapat dianggap sebagai operator yang didefinisikan dalam ruang fungsi.

Menggunakan transformasi Fourier, fungsi asli dapat ditulis sebagai berikut asalkan fungsi hanya memiliki jumlah diskontinuitas yang terbatas dan benar -benar dapat diintegrasikan.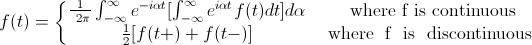

Apa perbedaan antara Laplace dan Transformasi Fourier?

• Transformasi Fourier dari suatu fungsi F (T) didefinisikan sebagai [latex] f (\\ alpha) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ infty^\\ infty e^i \\ alpha t f (t) dt [/latex], sedangkan transformasi laplace didefinisikan sebagai [laTex] f (s) = \\ int_ 0^\\ infty e^-st f (t) dt [/latex].
• Fourier Transform didefinisikan hanya untuk fungsi yang didefinisikan untuk semua bilangan real, sedangkan Transformasi Laplace tidak mengharuskan fungsi untuk didefinisikan pada mengatur bilangan real negatif.
• Transformasi Fourier adalah kasus khusus dari Transformasi Laplace. Dapat dilihat bahwa keduanya bertepatan untuk bilangan real non-negatif. (Saya.e. mengambil S di Laplace Iα + β Di mana α Dan β benar -benar nyata e ^β= ¹/_{√ (2ᴫ)})
• Setiap fungsi yang memiliki transformasi Fourier akan memiliki transformasi Laplace tetapi tidak sebaliknya.