Apa perbedaan antara metode Hartree dan Hartree-Fock

Itu Perbedaan utama antara metode Hartree dan Hartree-Fock adalah bahwa metode Hartree menggunakan fungsi gelombang bosonik, sedangkan metode Hartree-Fock menggunakan fungsi gelombang fermionik.

Kedua metode Hartree dan Hartree-Fock adalah metode lapangan yang konsisten sendiri mirip dengan teori fungsional kepadatan. Namun, kedua metode ini fokus pada dua jenis fungsi gelombang yang berbeda.

ISI

1. Ikhtisar dan Perbedaan Utama
2. Apa itu metode Hartree
3. Apa itu metode Hartree-Fock
4. Metode Hartree vs Hartree-Fock dalam bentuk tabel
5. Ringkasan - Metode Hartree vs Hartree -Fock

Apa itu metode Hartree?

Metode Hartree adalah metode yang digunakan dalam mendekati nilai energi dan fungsi gelombang sistem multi-elektron kuantum yang berada dalam keadaan stasioner. Diasumsikan bahwa fungsi gelombang N-body yang tepat dari sistem dapat diperkirakan oleh produk dari fungsi gelombang elektron tunggal. Menggunakan teknik ini, kita dapat menggunakan orbital N spin untuk memperoleh persamaan N-coupled yang berbeda untuk mereka. Selanjutnya, solusi untuk persamaan ini dapat menghasilkan fungsi gelombang Hartree dan energi sistem.

Menurut sistem mekanik kuantum sebelumnya, kita dapat memprediksi solusi yang tepat dari multi-elektron. Persamaan Schrodinger berisi sekelompok fungsi gelombang multi-elektron. Masing -masing fungsi gelombang ini memiliki nilai eigen energi terkait. Selain itu, fungsi gelombang dan nilai energi ini cenderung menggambarkan keadaan dasar dan keadaan tereksitasi atom multi-elektron karena fungsi gelombang hidrogen dan energi yang terkait digunakan untuk menjelaskan keadaan dasar dan keadaan tereksitasi dari atom hidrogen. Oleh karena itu, kita dapat memprediksi bahwa angka kuantum juga terlibat.

Metode Hartree diperkenalkan oleh Douglas Hartree pada tahun 1948 sebagai metode terbaik untuk menemukan fungsi gelombang satu elektron terbaik. Dua tahun kemudian, Vladimir Fock juga bereksperimen dengan metode ini, yang mengarah pada penemuan metode Hartree-Fock.

Apa itu metode Hartree-Fock?

Metode Hartree-Fock adalah metode yang mendekati kemampuan untuk menentukan energi dan fungsi gelombang dari sistem banyak tubuh kuantum. Ini ditentukan tentang keadaan stasioner. Istilah ini terutama digunakan dalam fisika dan kimia komputasi. Selain itu, metode ini sering cenderung mengasumsikan bahwa fungsi gelombang N-body yang tepat dari sistem tertentu dapat diperkirakan menggunakan penentu slater tunggal orbital N-spin. Selanjutnya, solusi dari persamaan ini dapat menghasilkan fungsi gelombang Hartree-Fock dan energi sistem.

Aplikasi khas dari metode Hartree-Fock termasuk menurunkan larutan persamaan Schrodinger untuk atom, molekul, struktur nano, dan padatan. Namun, ia juga memiliki penggunaan luas dalam fisika nuklir. Lebih lanjut, dalam teori struktur atom, perhitungan yang melibatkan spektrum dengan banyak tingkat energi tereksitasi juga memiliki aplikasi metode Hartree-Fock. Selain itu, ini adalah titik awal utama untuk banyak metode yang menggambarkan banyak sistem elektron jauh lebih akurat.

Apa perbedaan antara metode Hartree dan Hartree-Fock?

Metode Hartree dan metode Hartree-Fock adalah konsep penting yang terkait satu sama lain. Perbedaan utama antara metode Hartree dan Hartree-Fock adalah bahwa metode Hartree menggunakan fungsi gelombang bosonik, sedangkan metode Hartree-Fock menggunakan fungsi gelombang fermionik.

Infografis di bawah ini menyajikan perbedaan antara metode Hartree dan Hartree-Fock dalam bentuk tabel untuk perbandingan berdampingan.

Ringkasan -Metode Hartree vs Hartree -Fock

Metode Hartree adalah metode yang digunakan dalam mendekati nilai energi dan fungsi gelombang sistem multi-elektron kuantum yang berada dalam keadaan stasioner. Metode Hartree-Fock adalah metode yang mendekati kemampuan untuk menentukan energi dan fungsi gelombang dari sistem banyak tubuh kuantum. Perbedaan utama antara metode Hartree dan Hartree-Fock adalah bahwa metode Hartree menggunakan fungsi gelombang bosonik, sedangkan metode Hartree-Fock menggunakan fungsi gelombang fermionik.

Referensi:

1. “8.3: Persamaan Hartree-Fock diselesaikan dengan metode bidang yang konsisten diri." Libreteks Kimia, Libretexts, 11 Agustus. 2020.

Gambar milik:

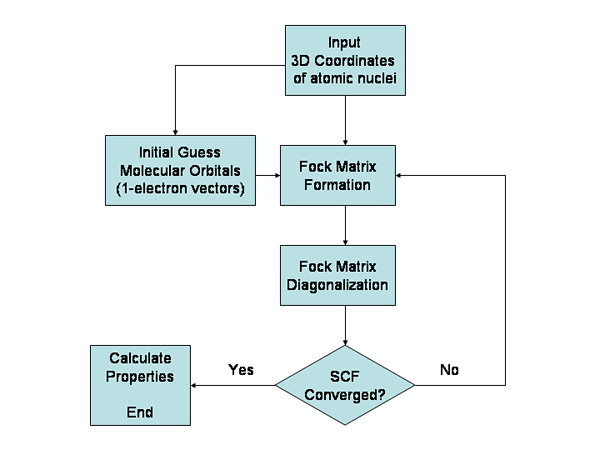
1. "Hartree-Fock" oleh Edsanville di English Wikipedia-karya sendiri oleh pengunggah asli (CC BY-SA 3.0) Via Commons Wikimedia