Perbedaan antara integrasi dan penjumlahan

Integrasi vs penjumlahan
 

Di atas matematika sekolah menengah, integrasi dan penjumlahan sering ditemukan dalam operasi matematika. Mereka tampaknya digunakan sebagai alat yang berbeda dan dalam situasi yang berbeda, tetapi mereka berbagi hubungan yang sangat dekat.

Lebih lanjut tentang penjumlahan

Penjumlahan adalah pengoperasian penambahan urutan angka dan operasi sering dilambangkan dengan surat bahasa Yunani Sigma σ. Ini digunakan untuk menyingkat penjumlahan dan sama dengan jumlah/total urutan. Mereka sering digunakan untuk mewakili seri, yang pada dasarnya adalah urutan tak terbatas yang disimpulkan. Mereka juga dapat digunakan untuk menunjukkan jumlah vektor, matriks, atau polinomial.

Penjumlahan biasanya dilakukan untuk berbagai nilai yang dapat diwakili oleh istilah umum, seperti seri yang memiliki istilah umum. Titik awal dan titik akhir penjumlahan dikenal sebagai batas bawah dan batas atas penjumlahan, masing -masing.

Misalnya, jumlah urutan a₁, A₂, A₃, A₄, … , A_N adalah₁ + A₂ + A₃ +... + a_N yang dapat dengan mudah diwakili menggunakan notasi penjumlahan sebagai ∑^N_{i = 1} A_Saya; Saya disebut indeks penjumlahan.

Banyak variasi yang digunakan untuk penjumlahan berdasarkan aplikasi. Dalam beberapa kasus, batas atas dan batas bawah dapat diberikan sebagai interval atau rentang, seperti ∑_1≤i≤100 A_Saya dan ∑_{i∈ [1.100]} A_Saya. Atau dapat diberikan sebagai satu set angka seperti ∑_i∈P A_Saya , dimana p adalah set yang ditentukan.

Dalam beberapa kasus, dua atau lebih tanda Sigma dapat digunakan, tetapi mereka dapat digeneralisasi sebagai berikut; ∑_J ∑_k A_jk = ∑_{J, k} A_jk.

Juga, penjumlahan mengikuti banyak aturan aljabar. Karena operasi tertanam adalah penambahan, banyak aturan umum aljabar dapat diterapkan pada jumlah itu sendiri dan untuk istilah individu yang digambarkan oleh penjumlahan.

Lebih lanjut tentang integrasi

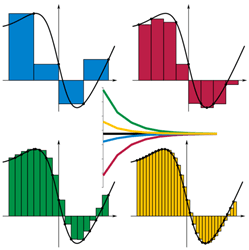
Integrasi didefinisikan sebagai proses diferensiasi sebaliknya. Tetapi dalam tampilan geometrisnya juga dapat dianggap sebagai area yang tertutup oleh kurva fungsi dan sumbu. Oleh karena itu, perhitungan area memberikan nilai integral yang pasti seperti yang ditunjukkan dalam diagram.

Sumber Gambar: http: // en.Wikipedia.org/wiki/file: riemann_sum_convergence.png

Nilai integral yang pasti sebenarnya adalah jumlah dari strip kecil di dalam kurva dan sumbu. Area setiap strip adalah tinggi × lebar pada titik pada sumbu yang dipertimbangkan. Lebar adalah nilai yang dapat kita pilih, katakanlah ∆x. Dan tinggi kira -kira nilai fungsi pada titik yang dipertimbangkan, katakanlah F(X_Saya). Dari diagram, terbukti bahwa semakin kecil strip yang lebih baik strip yang pas di dalam area yang dibatasi, sehingga perkiraan nilai yang lebih baik.

Jadi, secara umum integral yang pasti SAYA, di antara poin A dan B (i.e dalam interval [a, b] di mana aSAYA ≅ F(X₁) ∆x + F(X₂) ∆x + ⋯ + F(X_N) ∆x, di mana n adalah jumlah strip (n = (b-a)/∆x). Penjumlahan area ini dapat dengan mudah diwakili dengan menggunakan notasi penjumlahan sebagai SAYA ≅ ∑^N_{i = 1} F(X_Saya) ∆x. Karena perkiraan lebih baik ketika ∆x lebih kecil, kita dapat menghitung nilai saat ∆x → 0. Karena itu, masuk akal untuk mengatakannya SAYA = lim_{∆x → 0} ∑^N_{i = 1} F(X_Saya) ∆x.

Sebagai generalisasi dari konsep di atas, kita dapat memilih ∆x berdasarkan interval yang dipertimbangkan diindeks oleh I (memilih lebar area berdasarkan posisi). Lalu kita dapatkan

SAYA= lim_{∆x → 0} ∑^N_{i = 1} F(X_Saya) ∆x_Saya = _A∫^B F(x) dx

Ini dikenal sebagai reimann integral dari fungsi F(x) dalam interval [a, b]. Dalam hal ini A dan B dikenal sebagai batas atas dan batas bawah integral. Reimann Integral adalah bentuk dasar dari semua metode integrasi.

Intinya, integrasi adalah penjumlahan dari area ketika lebar persegi panjang sangat kecil.

Apa perbedaan antara integrasi dan penjumlahan?

• Penjumlahan menambah urutan angka. Biasanya, penjumlahan diberikan dalam bentuk ini^N_{i = 1} A_Saya Ketika istilah dalam urutan memiliki pola dan dapat diekspresikan menggunakan istilah umum.

• Integrasi pada dasarnya adalah area yang dibatasi oleh kurva fungsi, sumbu dan batas atas dan bawah. Area ini dapat diberikan sebagai jumlah area yang jauh lebih kecil yang termasuk dalam area yang dibatasi.

• Penjumlahan melibatkan nilai -nilai diskrit dengan batas atas dan bawah, sedangkan integrasi melibatkan nilai kontinu.

• Integrasi dapat diartikan sebagai bentuk penjumlahan khusus.

• Dalam metode perhitungan numerik, integrasi selalu dilakukan sebagai penjumlahan.