Perbedaan antara persamaan diferensial linier dan nonlinier

Persamaan diferensial linier vs nonlinier
Persamaan yang mengandung setidaknya satu koefisien diferensial atau turunan dari variabel yang tidak diketahui dikenal sebagai persamaan diferensial. Persamaan diferensial dapat berupa linier atau non-linear. Ruang lingkup artikel ini adalah untuk menjelaskan apa itu persamaan diferensial linier, apa persamaan diferensial nonlinier, dan apa perbedaan antara persamaan diferensial linier dan nonlinier.
Sejak pengembangan kalkulus di abad ke -18 oleh ahli matematika seperti Newton dan Leibnitz, persamaan diferensial telah memainkan peran penting dalam kisah matematika. Persamaan diferensial sangat penting dalam matematika karena berbagai aplikasi. Persamaan diferensial adalah jantung dari setiap model yang kami kembangkan untuk menjelaskan skenario atau peristiwa apa pun di dunia apakah itu dalam fisika, teknik, kimia, statistik, analisis keuangan, atau biologi (daftarnya tidak terbatas). Faktanya, sampai kalkulus menjadi teori yang sudah mapan, alat matematika yang tepat tidak tersedia untuk menganalisis masalah yang menarik di alam.
Persamaan yang dihasilkan dari aplikasi kalkulus tertentu mungkin sangat kompleks dan terkadang tidak dapat dipecahkan. Namun, ada yang bisa kita selesaikan, tetapi mungkin terlihat sama dan membingungkan. Oleh karena itu, untuk persamaan diferensial identifikasi yang lebih mudah dikategorikan oleh perilaku matematika mereka. Linear dan Nonlinear adalah salah satu kategorisasi tersebut. Penting untuk mengidentifikasi perbedaan antara persamaan diferensial linier dan nonlinier.
Apa persamaan diferensial linier?
Seandainya F: x → y Dan f (x) = y, a Persamaan diferensial tanpa istilah nonlinier dari fungsi yang tidak diketahui y dan turunannya dikenal sebagai persamaan diferensial linier.
Itu memaksakan kondisi bahwa y tidak dapat memiliki istilah indeks yang lebih tinggi seperti y2, y3,… Dan kelipatan turunan seperti
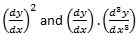
Itu juga tidak dapat mengandung istilah non linier seperti dosa y, ey^-2, atau ln y. Itu mengambil formulir,
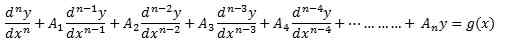
Di mana y Dan G adalah fungsi X. Persamaannya adalah persamaan diferensial keteraturan N, yang merupakan indeks turunan orde tertinggi.
Dalam persamaan diferensial linier, operator diferensial adalah operator linier dan solusi membentuk ruang vektor. Sebagai hasil dari sifat linier dari set solusi, kombinasi linier dari solusi juga merupakan solusi untuk persamaan diferensial. Yaitu, jika y1 Dan y2 adalah solusi dari persamaan diferensial, kemudian C1 y1+ C2 y2 juga merupakan solusi.
Linearitas persamaan hanyalah satu parameter klasifikasi, dan selanjutnya dapat dikategorikan ke dalam persamaan diferensial yang homogen atau non-homogen dan biasa atau parsial. Jika fungsinya G= 0 maka persamaannya adalah persamaan diferensial homogen linier. Jika F adalah fungsi dari dua atau lebih variabel independen (f: x, t → y) Dan f (x, t) = y , maka persamaannya adalah persamaan diferensial parsial linier.
Metode solusi untuk persamaan diferensial tergantung pada jenis dan koefisien persamaan diferensial. Kasus termudah muncul ketika koefisiennya konstan. Contoh klasik untuk kasus ini adalah hukum gerak kedua Newton dan berbagai aplikasinya. Hukum kedua Newton menghasilkan persamaan diferensial linier urutan kedua dengan koefisien konstan.
Apa persamaan diferensial nonlinier?
Persamaan yang mengandung istilah nonlinier dikenal sebagai persamaan diferensial non-linear.
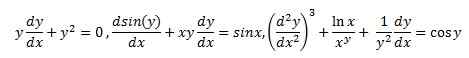
Semua di atas adalah persamaan diferensial nonlinier. Persamaan diferensial nonlinier sulit dipecahkan, oleh karena itu, studi dekat diperlukan untuk mendapatkan solusi yang benar. Dalam hal persamaan diferensial parsial, sebagian besar persamaan tidak memiliki solusi umum. Oleh karena itu, setiap persamaan harus diperlakukan secara mandiri.
Persamaan Navier-Stokes dan persamaan Euler dalam dinamika fluida, persamaan bidang relativitas umum Einstein adalah persamaan diferensial parsial nonlinier yang terkenal. Terkadang penerapan persamaan lagrange untuk sistem variabel dapat menghasilkan sistem persamaan diferensial parsial nonlinier.
Apa perbedaan antara persamaan diferensial linier dan nonlinier?
• Persamaan diferensial, yang hanya memiliki istilah linier dari variabel yang tidak diketahui atau dependen dan turunannya, dikenal sebagai persamaan diferensial linier. Tidak memiliki istilah dengan variabel dependen indeks lebih tinggi dari 1 dan tidak mengandung kelipatan dari turunannya. Ia tidak dapat memiliki fungsi nonlinier seperti fungsi trigonometri, fungsi eksponensial, dan fungsi logaritmik sehubungan dengan variabel dependen. Persamaan diferensial apa pun yang berisi istilah yang disebutkan di atas adalah persamaan diferensial nonlinier.
• Solusi persamaan diferensial linier menciptakan ruang vektor dan operator diferensial juga merupakan operator linier dalam ruang vektor.
• Solusi persamaan diferensial linier relatif lebih mudah dan ada solusi umum. Untuk persamaan nonlinier, dalam kebanyakan kasus, solusi umum tidak ada dan solusinya mungkin spesifik masalah. Ini membuat solusi jauh lebih sulit daripada persamaan linier.


