Perbedaan antara matriks dan penentu

Matriks vs penentu
 

Matriks dan penentu adalah konsep penting adalah aljabar linier, di mana matriks memberikan cara singkat untuk mewakili persamaan linier yang besar dan kombinasi sementara penentu secara unik terkait dengan jenis matriks tertentu.

Lebih banyak tentang matriks

Matriks adalah array persegi panjang angka di mana angka diatur dalam baris dan kolom. Jumlah kolom dan baris dalam matriks menentukan ukuran matriks. Secara umum, matriks secara identik diwakili oleh tanda kurung persegi, dan angka -angka diselaraskan dalam baris dan kolom di dalamnya.

A dikenal sebagai matriks 3 × 3 karena memiliki 3 kolom dan 3 baris. Angka -angka yang dilambangkan dengan A_IJ disebut elemen dan secara unik diidentifikasi oleh nomor baris dan nomor kolom. Juga, matriks dapat direpresentasikan sebagai [a_ij] _ (3 × 3), tetapi penggunaannya terbatas karena elemen tidak secara eksplisit diberikan. Memperluas contoh di atas ke kasus umum kita dapat menentukan matriks umum ukuran m × n;

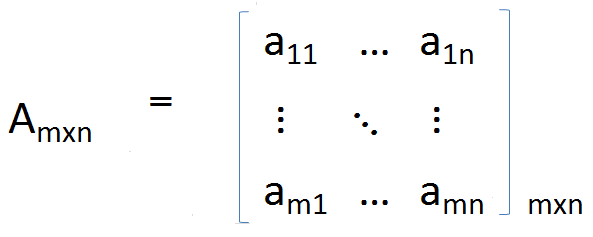
A memiliki baris m dan n kolom.

Matriks dikategorikan berdasarkan sifat khusus mereka. Sebagai contoh, matriks dengan jumlah baris dan kolom yang sama dikenal sebagai matriks persegi, dan matriks dengan kolom tunggal dikenal sebagai vektor.

Operasi pada matriks secara khusus didefinisikan tetapi mengikuti aturan dalam aljabar abstrak. Oleh karena itu, penambahan, pengurangan, dan perkalian antara matriks dilakukan pada elemen bijaksana. Untuk matriks, pembagian tidak ditentukan meskipun ada kebalikan.

Matriks adalah representasi singkat dari kumpulan angka, dan dapat dengan mudah digunakan untuk memecahkan persamaan linier. Matriks juga memiliki aplikasi luas di bidang aljabar linier, tentang transformasi linier.

Lebih lanjut tentang penentu

Penentu adalah angka unik yang terkait dengan setiap matriks kuadrat dan diperoleh setelah melakukan perhitungan tertentu untuk elemen dalam matriks. Dalam praktiknya, penentu dilambangkan dengan meletakkan tanda modulus untuk elemen dalam matriks. Oleh karena itu, penentu A diberikan oleh;

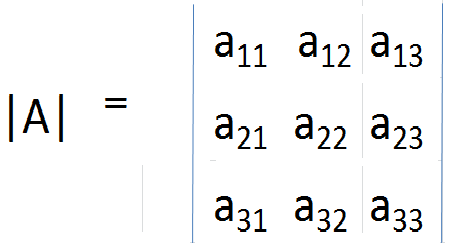
dan umumnya untuk matriks m × n

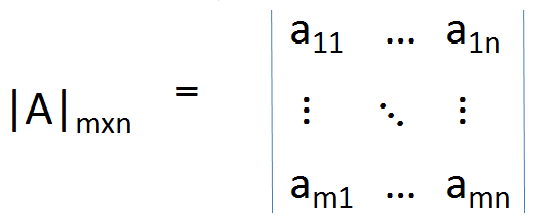
Operasi untuk mendapatkan penentu adalah sebagai berikut;

| A | = ∑^N_{j = 1} A_J C_{aku j}, dimana c_{aku j} adalah kofaktor matriks yang diberikan oleh c_{aku j} = (-1)^i+j M_{aku j}.

Penentu merupakan faktor penting yang menentukan sifat -sifat matriks. Jika penentu adalah nol untuk matriks tertentu, kebalikan dari matriks tidak ada.

Apa perbedaan antara matriks dan penentu?

• Matriks adalah sekelompok angka, dan penentu adalah angka unik yang terkait dengan matriks itu.

• Penentu dapat diperoleh dari matriks persegi, tetapi tidak sebaliknya. Penentu tidak dapat memberikan matriks unik yang terkait dengannya.

• Aljabar tentang matriks dan penentu memiliki kesamaan dan perbedaan. Apalagi saat melakukan penggandaan. Misalnya, multiplikasi matriks harus dilakukan elemen bijaksana, di mana penentu adalah angka tunggal dan mengikuti perkalian sederhana.

• Determinan digunakan untuk menghitung kebalikan dari matriks dan jika penentu nol kebalikan dari matriks tidak ada.