Perbedaan antara postulat dan teorema

Perbedaan Utama - Postulat VS Teorema
 

Deposulat dan Teorema adalah dua istilah umum yang sering digunakan dalam matematika. Postulat adalah pernyataan yang dianggap benar, tanpa bukti. Teorema adalah pernyataan yang dapat terbukti benar. Ini adalah perbedaan utama Antara Postulat dan Teorema. Teorema sering didasarkan pada dalil.

Apa itu Postulat?

Postulat adalah pernyataan yang dianggap benar tanpa bukti apa pun. Postulat didefinisikan oleh Kamus Oxford sebagai “hal yang disarankan atau dianggap benar sebagai dasar untuk penalaran, diskusi, atau kepercayaan” dan oleh Kamus Warisan Amerika sebagai “sesuatu yang diasumsikan tanpa bukti sebagai bukti yang jelas atau umumnya diterima, terutama ketika digunakan sebagai dasar argumen ”.

Deposulat juga dikenal sebagai aksioma. Postulat tidak harus dibuktikan karena mereka tampak benar. Misalnya, pernyataan bahwa dua poin membuat garis adalah postulat. Postulat adalah dasar dari mana teorema dan lemma dibuat. Teorema dapat diturunkan dari satu atau lebih postulat.

Di bawah ini adalah beberapa karakteristik dasar yang dimiliki semua postulat:

• Postulat harus mudah dimengerti - mereka seharusnya tidak memiliki banyak kata yang sulit dipahami.
• Mereka harus konsisten saat dikombinasikan dengan postulat lain.
• Mereka harus memiliki kemampuan untuk digunakan secara mandiri.

Namun, beberapa postulat - seperti postulat Einstein bahwa alam semesta homogen - tidak selalu benar. Postulat mungkin menjadi salah setelah penemuan baru.

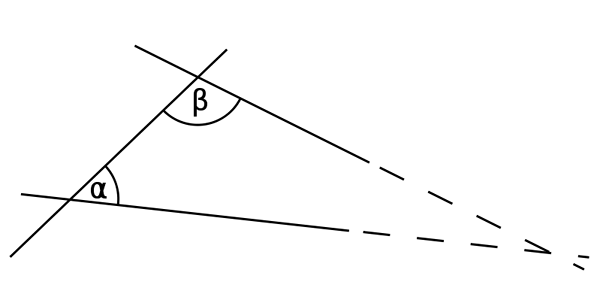
Jika jumlah sudut interior α dan β kurang dari 180 °, dua garis lurus, diproduksi tanpa batas waktu, bertemu di sisi itu.

Apa itu Teorema?

Teorema adalah pernyataan yang dapat terbukti benar. Kamus Oxford mendefinisikan teorema sebagai “proposisi umum tidak jelas tetapi dibuktikan dengan rantai penalaran; Sebuah kebenaran yang ditetapkan melalui kebenaran yang diterima "dan Merriam-Webster mendefinisikannya sebagai" formula, proposisi, atau pernyataan dalam matematika atau logika yang disimpulkan atau disimpulkan dari rumus atau proposisi lain ".

Teorema dapat dibuktikan dengan penalaran logis atau dengan menggunakan teorema lain yang telah terbukti benar.  Teorema yang harus dibuktikan untuk membuktikan bahwa teorema lain disebut a kata pengantar singkat. Baik lemma dan teorema didasarkan pada dalil. Teorema biasanya memiliki dua bagian yang dikenal sebagai hipotesis dan kesimpulan. Teorema Pythagoras, Empat Teorema Warna, dan Teorema Terakhir Fermat adalah beberapa contoh teorema.

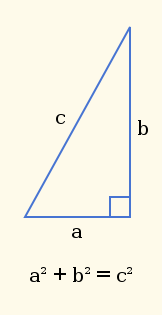
Visualisasi Teorema Pythagoras

Apa perbedaan antara postulat dan teorema?

Definisi:

Mendalilkan: Postulat didefinisikan sebagai “pernyataan yang diterima sebagai dasar untuk argumen atau inferensi."

Dalil: Teorema didefinisikan sebagai “proposisi umum tidak jelas tetapi dibuktikan dengan rantai penalaran; kebenaran yang ditetapkan melalui kebenaran yang diterima ”.

Bukti:

Mendalilkan: Postulat adalah pernyataan yang dianggap benar tanpa bukti apa pun.

Dalil: Teorema adalah pernyataan yang dapat terbukti benar.

Hubungan:

Mendalilkan: Deposulat adalah dasar untuk teorema dan lemma.

Dalil: Teorema didasarkan pada dalil.

Perlu membuktikan:

Mendalilkan: Deposulasi tidak perlu dibuktikan karena mereka menyatakan yang jelas.

Dalil:  Teorema dapat dibuktikan dengan penalaran logis atau dengan menggunakan teorema lain yang telah terbukti benar. 

Gambar milik:

"Teorema Pythagoras ABC" oleh Pythagoras ABC.PNG: NL: Gebruiker: Andre_engels - Pythagoras ABC.PNG (CC BY-SA 3.0) Via Commons Wikimedia

“Parallel Postulate EN” pada 6054 - sunting http: // pl.Wikipedia.org/wiki/grafika: paralel_postulate.SVG oleh Pengguna: Harkonnen2 (CC BY-SA 3.0) Via Commons Wikimedia