Perbedaan antara transpos dan matriks terbalik
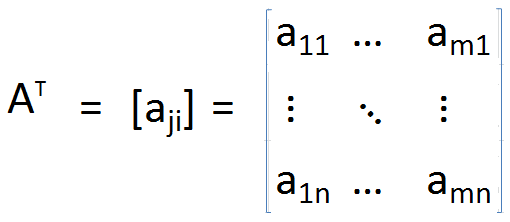
Transpose vs matriks terbalik
Transpose dan terbalik adalah dua jenis matriks dengan sifat khusus yang kami temui dalam matriks aljabar. Mereka berbeda satu sama lain, dan tidak berbagi hubungan dekat karena operasi yang dilakukan untuk mendapatkannya berbeda.
Mereka memiliki aplikasi yang luas di bidang aljabar linier dan implementasi yang diturunkan seperti ilmu komputer.
Lebih lanjut tentang matriks transpose
Transpose matriks A dapat diidentifikasi sebagai matriks yang diperoleh dengan mengatur ulang kolom sebagai baris atau baris sebagai kolom. Akibatnya, indeks masing -masing elemen dipertukarkan. Lebih formal, transpose matriks A, didefinisikan sebagai
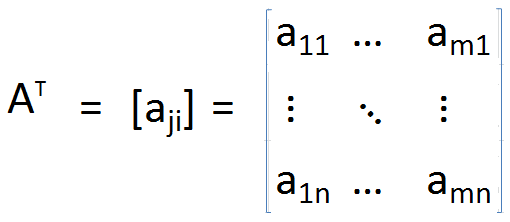
Di mana
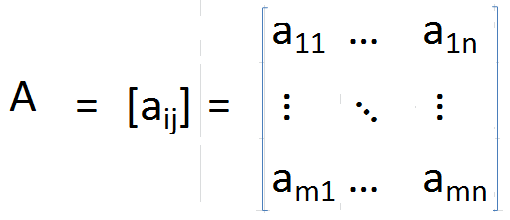
Dalam matriks transpos, diagonal tetap tidak berubah, tetapi semua elemen lainnya diputar di sekitar diagonal. Juga, ukuran matriks juga berubah dari m × n ke n × m.
Transpose memiliki beberapa sifat penting, dan mereka memungkinkan manipulasi matriks yang lebih mudah. Juga, beberapa matriks transpos penting didefinisikan berdasarkan karakteristiknya. Jika matriksnya sama dengan transpose, maka matriksnya simetris. Jika matriks sama dengan negatif dari transpos, matriks adalah simetris miring. Transpos konjugat dari suatu matriks adalah transpos dari matriks dengan elemen diganti dengan konjugat kompleksnya.
Lebih lanjut tentang matriks terbalik
Invers dari suatu matriks didefinisikan sebagai matriks yang memberikan matriks identitas saat dikalikan bersama. Oleh karena itu, menurut definisi, jika Ab = ba = i Kemudian B adalah matriks terbalik dari A Dan A adalah matriks terbalik dari B. Jadi, jika kami mempertimbangkan B = A-1 , Kemudian A A-1 = A-1A = i
Agar matriks dapat dibalik, kondisi yang diperlukan dan cukup adalah penentu dari A bukan nol; Saya.E |A| = det (A) ≠ 0. Matriks dikatakan tidak dapat dibalik, non-singular, atau non-degeneratif jika memenuhi kondisi ini. Itu mengikuti itu A adalah matriks persegi dan keduanya A-1 Dan A memiliki ukuran yang sama.
Kebalikan dari matriks A dapat dihitung dengan banyak metode dalam aljabar linier seperti eliminasi Gaussian, komposisi eigendecomposition, dekomposisi Cholesky, dan aturan Carmer. Matriks juga dapat dibalik dengan metode inversi blok dan seri Neuman.
Apa perbedaan antara transpos dan matriks terbalik?
• Transpose diperoleh dengan mengatur ulang kolom dan baris dalam matriks sementara terbalik diperoleh dengan komputasi numerik yang relatif sulit. (Tetapi pada kenyataannya keduanya adalah transformasi linier)
• Sebagai hasil langsung, elemen -elemen dalam transpos hanya mengubah posisi mereka, tetapi nilainya sama. Namun di terbalik, angkanya bisa sangat berbeda dari matriks asli.
• Setiap matriks dapat memiliki transpos, tetapi kebalikannya hanya didefinisikan untuk matriks persegi, dan penentu harus menjadi penentu yang tidak nol.


