Perbedaan antara rata -rata, median dan mode

Berarti vs median vs mode
 

Berarti, median, dan mode adalah yang utama Ukuran kecenderungan sentral digunakan dalam statistik deskriptif. Mereka benar -benar berbeda satu sama lain dan kasus di mana mereka digunakan untuk merangkum data juga berbeda.

Berarti

Rata -rata aritmatika adalah jumlah dari nilai data yang dibagi dengan jumlah nilai data, i.e.

[latex] \ bar x = \ frac 1 n \ sum_ i = 1^n x_ i = \ frac x_ 1+x_ 2+x_ 3 +... +x_ n n [/latex] 

Jika data berasal dari ruang sampel itu disebut rata -rata sampel ([latex] \ bar x [/latex]), yang merupakan statistik deskriptif dari sampel. Meskipun ini adalah ukuran deskriptif yang paling umum digunakan untuk sampel, ini bukan statistik yang kuat. Ini sangat sensitif terhadap outlier dan osilasi.

Misalnya, pertimbangkan pendapatan rata -rata warga kota tertentu. Karena semua nilai data dijumlahkan dan kemudian dibagi, pendapatan orang yang sangat kaya mempengaruhi rata -rata secara signifikan. Oleh karena itu, nilai rata -rata bukanlah representasi data yang baik selalu.

Juga, dalam kasus sinyal bergantian, arus yang melewati elemen secara berkala bervariasi dari arah positif ke arah negatif dan sebaliknya. Jika kita mengambil rata -rata arus melewati elemen dalam satu periode, itu akan memberikan 0, yang berarti bahwa tidak ada arus yang melewati elemen, yang jelas tidak benar. Oleh karena itu, dalam hal ini juga, rata -rata aritmatika bukanlah ukuran yang baik.

Rata -rata aritmatika adalah indikator yang baik ketika data didistribusikan secara merata. Untuk distribusi normal, rata -rata sama dengan mode dan median. Ini juga memiliki residu terendah saat mempertimbangkan kesalahan akar rata -rata kuadrat; Oleh karena itu, ukuran deskriptif terbaik saat diperlukan untuk mewakili dataset dengan satu nomor.

Median

Nilai titik data tengah setelah mengatur semua nilai data dalam urutan naik didefinisikan sebagai median dataset. Median adalah kuartil ke -2, desil ke -5 dan persentil ke -50.

• Jika jumlah pengamatan (titik data) ganjil, maka mediannya adalah pengamatan persis di tengah daftar yang dipesan.

• Jika jumlah pengamatan (titik data) genap, maka median adalah rata -rata dari dua pengamatan tengah dalam daftar yang dipesan.

Median membagi pengamatan menjadi dua kelompok; Saya.e. kelompok (50%) nilai lebih tinggi dan kelompok (50%) nilai lebih rendah dari median. Median secara khusus digunakan dalam distribusi miring dan mewakili data yang cukup lebih baik daripada rata -rata aritmatika.

Mode

Mode adalah angka yang paling banyak terjadi dalam serangkaian pengamatan. Mode set data dihitung dengan menemukan frekuensi setiap elemen dalam set.

• Jika tidak ada nilai yang terjadi lebih dari sekali, maka set data tidak memiliki mode.

• Jika tidak, nilai apa pun yang terjadi dengan frekuensi terbesar adalah mode set data.

Lebih dari 1 mode dapat ada dalam satu set; Oleh karena itu, mode bukanlah statistik unik dari dataset. Dalam distribusi yang seragam, ada satu mode. Mode distribusi probabilitas diskrit adalah titik di mana fungsi massa probabilitas mencapai titik tertinggi. Memberikan dari interpretasi di atas, kita dapat mengatakan itu Maxima Global adalah mode.

Pertimbangkan penerapan ketiga langkah ke kumpulan data berikut.

Data: 1, 1, 2, 3, 5, 5, 5, 5, 6, 6, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 14, 14, 15, 15 , 15

Rata -rata = (1+ 1+ 2+ 3+ 5+ 5+ 5+ 5+ 6+ 6+ 8+ 8+ 9+ 9+ 9+ 9+ 10+ 10+ 10+ 14+ 14+ 15+ 15+ 15+ ) / 25 = 8.12

Median = 9 (elemen ke -13)

Mode = 9 (frekuensi 9 = 5)

Apa perbedaan antara rata -rata, median dan mode?

• Rata -rata aritmatika adalah jumlah nilai (pengamatan) dibagi dengan jumlah pengamatan. Ini bukan statistik yang kuat, dan sangat tergantung pada sifat distribusi normal dalam distribusi yang dipertimbangkan. Pencilan tunggal dapat menyebabkan pergeseran yang signifikan dalam rata -rata memberikan nilai yang relatif menyesatkan. Konsep ini dapat diperluas ke rata -rata geometris, rata -rata harmonik, rata -rata tertimbang dan sebagainya.

• Median adalah nilai tengah dari rangkaian pengamatan, dan relatif kurang terpengaruh oleh outlier. Itu mungkin memberikan estimasi yang baik sebagai statistik ringkasan dalam kasus yang sangat miring.

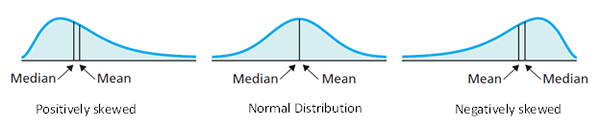
• Mode adalah nilai pengamatan yang paling umum dalam dataset. Jika distribusinya condong positif, mode terletak di kiri ke median dan, jika miring secara negatif, mode tersebut terletak tepat ke median.

• Jika condong positif, rata -rata benar untuk median; Jika rata -rata condong negatif adalah ke kiri median.

• Dalam distribusi normal, ketiganya, rata -rata, mode dan median adalah sama.