Perbedaan antara jajaran genjang dan trapesium

Jajaran genjang vs trapesium
 

Jajaran genjang dan trapesium (atau trapezium) adalah dua cembung segi empat cembung. Meskipun ini adalah segi empat, geometri trapesium berbeda secara signifikan dari jajaran genjang.

Genjang

Jajaran genjang dapat didefinisikan sebagai sosok geometris dengan empat sisi, dengan sisi yang berlawanan sejajar satu sama lain. Lebih tepatnya itu adalah segi empat dengan dua pasang sisi paralel. Sifat paralel ini memberikan banyak karakteristik geometris pada jajaran genjang.

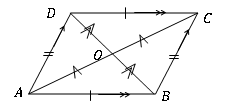
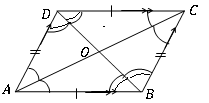
Sebuah segi empat adalah jajaran genjang jika berikut karakteristik geometris ditemukan.

• Dua pasang sisi yang berlawanan panjangnya sama. (AB = DC, AD = BC)

• Dua pasang sudut yang berlawanan memiliki ukuran yang sama. ([latex] d \ hat a b = b \ hat c d, a \ hat d c = a \ hat b c [/latex])

• Jika sudut yang berdekatan adalah tambahan [lateks] d \ hat a b + a \ hat d c = a \ hat d c + b \ hat c d = b \ topi c d + A \ hat b c = a \ hat b c + d \ hat a b = 180^\ circ = \ pi rad [/latex]

• Sepasang sisi, yang saling bertentangan, adalah paralel dan panjangnya sama. (AB = DC & AB∥DC)

• Diagonal saling membagi dua (ao = oc, bo = od)

• Setiap diagonal membagi segi empat menjadi dua segitiga kongruen. (∆ADB ≡ ∆BCD, ∆ABC ≡ ∆ADC)

Selanjutnya, jumlah kotak sisi sama dengan jumlah kotak diagonal. Ini terkadang disebut sebagai hukum jajaran genjang dan memiliki aplikasi luas dalam fisika dan teknik. (AB² + Bc² + CD² + Da² = Ac² + Bd²)

Masing -masing karakteristik di atas dapat digunakan sebagai properti, setelah ditetapkan bahwa segi empat adalah jajaran genjang.

Luas jajaran genjang dapat dihitung dengan produk dari panjang satu sisi dan tinggi ke sisi yang berlawanan. Oleh karena itu, luas jajaran genjang dapat dinyatakan sebagai

Area jajaran genjang = basis × tinggi = AB×H

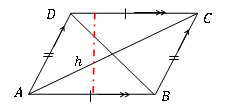
Area jajaran genjang tidak tergantung pada bentuk jajaran genjang individu. Itu hanya tergantung pada panjang dasar dan ketinggian tegak lurus.

Jika sisi jajaran genjang dapat diwakili oleh dua vektor, area tersebut dapat diperoleh dengan besarnya produk vektor (produk lintas) dari dua vektor yang berdekatan.

Jika sisi AB dan AD diwakili oleh vektor ([lateks] \ overrighrowrow ab [/latex]) dan ([latex] \ overrighrowrow ad [/latex]) masing -masing, area jajaran genjang diberikan oleh [ lateks] \ kiri | \ OverrighArtArrow ab \ Times \ OverrighArtarrow ad \ right | = Ab \ cdot ad \ sin \ alpha [/latex], di mana α adalah sudut antara [lateks] \ overrighrighrow ab [/lateks] dan [lateks] \ overrighrowrow ad [/latex]. 

Berikut ini adalah beberapa sifat canggih dari jajaran genjang;

• Luas jajaran genjang adalah dua kali luas segitiga yang dibuat oleh diagonalnya.

• Area jajaran genjang dibagi menjadi dua dengan garis apa pun yang melewati titik tengah.

• Setiap transformasi afin non-degenerasi membutuhkan jajaran genjang ke jajaran genjang lain

• Garis generasi memiliki simetri rotasi urutan 2

• Jumlah jarak dari titik interior setiap jajaran genjang ke sisi tidak tergantung pada lokasi titik

Trapesium

Trapesium (atau Trapezium dalam bahasa Inggris Inggris) adalah cembung segi empat di mana setidaknya dua sisi paralel dan panjangnya tidak setara. Sisi paralel trapesium dikenal sebagai pangkalan dan dua sisi lainnya disebut kaki.

Berikut ini adalah karakteristik utama trapesium;

• Jika sudut yang berdekatan tidak berada di dasar trapesium yang sama, mereka adalah sudut tambahan. Saya.e. Mereka menambahkan hingga 180 ° ([lateks] b \ topi a d+a \ hat d c = a \ hat b c+b \ hat c d = 180^\ circ [// getah])

• Kedua diagonal trapesium berpotongan pada rasio yang sama (rasio antara bagian diagonal adalah sama).

• Jika A dan B adalah basis dan C, D adalah kaki, panjang diagonal diberikan oleh  

[latex] \ sqrt \ frac ab^2 -a^2 b-ac^2+bd^2 b-a [/latex] 

Dan

[latex] \ sqrt \ frac ab^2 -a^2 b-ac^2+bc^2 b-a [/latex]

Area trapesium dapat dihitung dengan menggunakan rumus berikut

Area trapesium = [latex] \ frac a+b 2 \ kali h [/latex]

Apa perbedaan antara jajaran genjang dan trapesium (trapezium)?

• Baik jajaran genjang dan trapesium adalah cembung segiempat.

• Dalam jajaran genjang, kedua pasangan sisi yang berlawanan adalah paralel sementara, dalam trapesium, hanya sepasang yang paralel.

• Diagonal jajaran genjang saling membagi dua (rasio 1: 1) sedangkan diagonal trapesium berpotongan dengan rasio konstan antara bagian.

• Area jajaran genjang tergantung pada ketinggian dan dasar sedangkan luas trapesium tergantung pada tinggi dan segmen tengah.

• Dua segitiga yang dibentuk oleh diagonal dalam jajaran genjang selalu kongruen sedangkan segitiga trapesium bisa kongruen atau tidak.